Как определить координаты центра тяжести плоской фигуры. Нахождение центра тяжести своего тела. «Решение задач комплексного характера»
Определение центра тяжести произвольного тела путем последовательного сложения сил, действующих на отдельные его части,- трудная задача; она облегчается только для тел сравнительно простой формы.
Пусть тело состоит только из двух грузов массы и , соединенных стрежнем (рис. 125). Если масса стержня мала по сравнению с массами и , то ею можно пренебречь. На каждую из масс действуют силы тяжести, равные соответственно и ; обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы знаем, равнодействующая двух параллельных сил приложена в точке , которая определяется из условия

Рис. 125. Определение центра тяжести тела, состоящего из двух грузов
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Если это тело подвесить в точке , оно останется в равновесии.
Так как две равные массы имеют общий центр тяжести в точке, делящей пополам расстояние между этими массами, то сразу ясно, что, например, центр тяжести однородного стержня лежит в середине стержня (рис. 126).
Поскольку любой диаметр однородного круглого диска делит его на две совершенно одинаковые симметричные части (рис. 127), то центр тяжести должен лежать на каждом диаметре диска, т. е. в точке пересечения диаметров - в геометрическом центре диска . Рассуждая сходным образом, можно найти, что центр тяжести однородного шара лежит в его геометрическом центре, центр тяжести однородного прямоугольного параллелепипеда лежит на пересечении его диагоналей и т. д. Центр тяжести обруча или кольца лежит в его центре. Последний пример показывает, что центр тяжести тела может лежать вне тела.

Рис. 126. Центр тяжести однородного стержня лежит в его середине

Рис. 127. Центр однородного диска лежит в его геометрическом центре
Если тело имеет неправильную форму или если оно неоднородно (например, в нем есть пустоты), то расчет положения центра тяжести часто затруднителен и это положение удобнее найти посредством опыта. Пусть, например, требуется найти центр тяжести куска фанеры. Подвесим его на нити (рис. 128). Очевидно, в положении равновесия центр тяжести тела должен лежать на продолжении нити, иначе сила тяжести будет иметь момент относительно точки подвеса, который начал бы вращать тело. Поэтому, проведя на нашем куске фанеры прямую, представляющую продолжение нити, можем утверждать, что центр тяжести лежит на этой прямой.
Действительно, подвешивая тело в разных точках и проводя вертикальные прямые, мы убедимся, что все они пересекутся в одной точке. Эта точка и есть центр тяжести тела (так как он должен лежать одновременно на всех таких прямых). Подобным образом можно определить положение центра тяжести не только плоской фигуры, но и более сложного тела. Положение центра тяжести самолета определяют, вкатывая его колесами на платформы весов. Равнодействующая сил веса, приходящихся на каждое колесо, будет направлена по вертикали, и найти линию, по которой она действует, можно по закону сложения параллельных сил.

Рис. 128. Точка пересечения вертикальных линий, проведенных через точки подвеса и есть центр тяжести тела
При изменении масс отдельных частей тела или при изменении формы тела положение центра тяжести меняется. Так, центр тяжести самолета перемещается при расходовании горючего из баков, при загрузке багажа и т. п. Для наглядного опыта, иллюстрирующего перемещение центра тяжести при изменении формы тела, удобно взять два одинаковых бруска, соединенных шарниром (рис. 129). В том случае, когда бруски образуют продолжение один другого, центр тяжести лежит на оси брусков. Если бруски согнуть в шарнире, то центр тяжести оказывается вне брусков, на биссектрисе угла, который они образуют. Если на один из брусков надеть дополнительный груз, то центр тяжести переместится в сторону этого груза.

Рис. 129. а) Центр тяжести соединенных шарниром брусков, расположенных на одной прямой, лежит на оси брусков, б) Центр тяжести согнутой системы брусков лежит вне брусков
81.1. Где находится центр тяжести двух одинаковых тонких стержней, имеющих длину 12 см и скрепленных в виде буквы Т?
81.2. Докажите, что центр тяжести однородной треугольной пластины лежит на пересечении медиан.

Рис. 130. К упражнению 81.3
81.3. Однородная доска массы 60 кг лежит на двух опорах, как показано на рис. 130. Определите силы, действующие на опоры.
Прямоугольник.
Так
как прямоугольник имеет две оси симметрии, то его центр тяжести находится на
пересечении осей симметрии, т.е. в точке
пересечения диагоналей прямоугольника.

Треугольник.
Центр
тяжести лежит в точке пересечения его
медиан. Из геометрии известно, что
медианы треугольника пересекаются в
одной точке и делятся в отношении 1:2 от
основания. 
Круг. Так как круг имеет две оси симметрии, то его центр тяжести находится на пересечении осей симметрии.
Полукруг.
Полукруг
имеет одну ось симметрии, то центр
тяжести лежит на этой оси. Другая
координата центра тяжести вычисляется
по формуле:
.

Многие конструктивные элементы изготавливают из стандартного проката – уголков, двутавров, швеллеров и других. Все размеры, а так же геометрические характеристики прокатных профилей это табличные данные, которые можно найти в справочной литературе в таблицах нормального сортамента (ГОСТ 8239-89, ГОСТ 8240-89).



Пример 1. Определить положение центра тяжести фигуры, представленной на рисунке.
Решение:

Выбираем оси координат, так чтобы ось Ох прошла по крайнему нижнему габаритному размеру, а ось Оу – по крайнему левому габаритному размеру.
Разбиваем сложную фигуру на минимальное количество простых фигур:
прямоугольник 20х10;
треугольник 15х10;
круг R=3 см.
Вычисляем площадь каждой простой фигуры, её координаты центра тяжести. Результаты вычислений заносим в таблицу
|
№ фигуры |
Площадь фигуры А, |
Координаты центра тяжести |
|
|
| |||
Ответ: С(14,5; 4,5)
Пример
2
.
Определить координаты центра тяжести
составного сечения, состоящего из листа
и прокатных профилей.

Решение.
Выбираем оси координат, так как показано на рисунке.
Обозначим фигуры номерами и выпишем из таблицы необходимые данные:
|
№ фигуры |
Площадь фигуры А, |
Координаты центра тяжести |
|
|
|
|||
|
|
|||
Вычисляем координаты центра тяжести фигуры по формулам:
Ответ: С(0; 10)
Лабораторная работа №1 «Определение центра тяжести составных плоских фигур»
Цель: Определить центр тяжести заданной плоской сложной фигуры опытным и аналитическим способами и сравнить их результаты.
Порядок выполнения работы
Разбить фигуру на минимальное количество фигур, центры тяжести которых, мы знаем, как определить.
Указать номера площадей и координаты центра тяжести каждой фигуры.
Вычислить координаты центра тяжести каждой фигуры.
Вычислить площадь каждой фигуры.
Вычислить координаты центра тяжести всей фигуры по формулам (положение центра тяжести нанести на чертеж фигуры):
Начертить в тетрадях свою плоскую фигуру по размерам, с указанием осей координат.
Определить центр тяжести аналитическим способом.
Установка
для опытного определения координат
центра тяжести способом подвешивания
состоит из вертикальной стойки 1
(см. рис.), к которой прикреплена игла 2
.
Плоская фигура 3
изготовлена из картона, в котором легко
проколоть отверстие. Отверстия А
и В
прокалываются в произвольно расположенных
точках (лучше на наиболее удаленном
расстоянии друг от друга). Плоская фигура
подвешивается на иглу сначала в точке
А
,
а потом в точке В
.
При помощи отвеса 4
,
закрепленного на той же игле, на фигуре
прочерчивают карандашом вертикальную
линию, соответствующую нити отвеса.
Центр тяжести С
фигуры будет находиться в точке
пересечения вертикальных линий,
нанесенных при подвешивании фигуры в
точках А
и В
.

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).
Радиус-вектор этой точки

Рисунок 1.6
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.
Если удельный вес однородного тела γ , вес элементарной частицы тела
P k = γΔV k (P = γV ) подставить в формулу для определения r C , имеем
Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а)


Рисунок 1.7
Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б)

Способы определения координат центра тяжести
Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
1 Аналитический (путем интегрирования).
2 Метод симметрии . Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела).
4 Разбиение . Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S 1 и S 2 (S = S 1 + S 2 ). Центры тяжести этих фигур находятся в точках C 1 (x 1 , y 1 ) и C 2 (x 2 , y 2 ) . Тогда координаты центра тяжести тела равны


Рисунок 1.8
5Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):


Рисунок 1.9
Центры тяжести простейших фигур

Рисунок 1.10
1 Треугольник
Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок 1.10, а).
DM = MB , CM = (1/3)AM .
2 Дуга окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. y C = 0 .

dl – элемент дуги, dl = Rdφ , R – радиус окружности, x = Rcosφ , L = 2αR ,
Следовательно:
x C = R(sinα/α) .
3 Круговой сектор
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox , на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R .
Центр тяжести сектора совпадает с центром тяжести дуги AB :
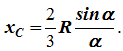
14. Способы задания движения точки.
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t . Чтобы записать ее уравнение в явной форме, надо исключить из них t .
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t) . Этим способом удобно пользоваться, если траектория точки заранее известна.
15. 1.2 Скорость точки
Рассмотрим перемещение точки за малый промежуток времени Δt :
![]()
средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени


Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
Учебник для 7 класса
§ 25.3. Как найти центр тяжести тела?
Напомним, что центром тяжести называют точку приложения силы тяжести. Рассмотрим, как найти на опыте положение центра тяжести плоского тела - скажем, вырезанной из картона фигуры произвольной формы (см. лабораторную работу № 12).
Подвесим картонную фигуру с помощью булавки или гвоздя так, чтобы она могла свободно вращаться вокруг горизонтальной оси, проходящей через точку О (рис. 25.4, а). Тогда эту фигуру можно рассматривать как рычаг с точкой опоры О.
Рис. 25.4. Как найти на опыте центр тяжести плоской фигуры
Когда фигура находится в равновесии, действующие на нее силы уравновешивают друг друга. Это сила тяжести F т, приложенная в центре тяжести фигуры Т, и сила упругости F упр, приложенная в точке О (эта сила приложена со стороны булавки или гвоздя).
Эти две силы уравновешивают друг друга только при условии, что точки приложения этих сил (точки Т и О) лежат на одной вертикали (см. рис. 25.4, а). В противном случае сила тяжести будет поворачивать фигуру вокруг точки О (рис. 25.4, б).
Итак, когда фигура находится в равновесии, центр тяжести лежит на одной вертикали с точкой подвеса О. Это и позволяет определить положение центра тяжести фигуры. Проведем с помощью отвеса вертикаль, проходящую через точку подвеса (синяя линия на рис. 25.4, в). На проведенной линии лежит центр тяжести тела. Повторим этот опыт при другом положении точки подвеса. В результате мы получим вторую линию, на которой лежит центр тяжести тела (зеленая линия на рис. 25.4, г). Следовательно, на пересечении этих линий находится искомый центр тяжести тела (красная точка Г на рис. 25.4, г).
Автор : Возьмем тело произвольной формы. Можно ли подвесить его на нити так, чтобы оно после подвешивания сохранило свое положение (т.е. не стало поворачиваться) при любой начальной ориентации (рис. 27.1)?
Иными словами, существует ли такая точка, относительно которой сумма моментов сил тяжести, действующих на различные части тела, была бы равна нулю при любой ориентации тела в пространстве?
Читатель : По-моему, да. Такая точка называется центром тяжести тела.
Доказательство. Для простоты рассмотрим тело в виде плоской пластины произвольной формы произвольным образом ориентированное в пространстве (рис. 27.2). Возьмем систему координат х 0у с началом в центре масс – точке С , тогда х С = 0, у С = 0.
 Представим это тело в виде совокупности большого числа точечных масс m i
, положение каждой из которых задается радиусом-вектором .
Представим это тело в виде совокупности большого числа точечных масс m i
, положение каждой из которых задается радиусом-вектором .
По определению центра масс , а координата х С = .
Так как в принятой нами системе координат х С = 0, то . Умножим это равенство на g и получим
Как видно из рис. 27.2, |x i | – это плечо силы . Причем если х i > 0, то момент силы M i > 0, а если х j < 0, то M j < 0, поэтому с учетом знака можно утверждать, что для любого x i момент силы будет равен M i = m i gx i . Тогда равенство (1) эквивалентно равенству , где M i – момент силы тяжести . А это значит, что при произвольной ориентации тела сумма моментов сил тяжести, действующих на тело, будет равна нулю относительно его центра масс.
Чтобы рассматриваемое нами тело находилось в равновесии, к нему необходимо приложить в точке С силу Т = mg , направленную вертикально вверх. Момент этой силы относительно точки С равен нулю.
Поскольку наши рассуждения никак не зависели от того, как именно ориентировано тело в пространстве, мы доказали, что центр тяжести совпадает с центром масс, что и требовалось доказать.
Задача 27.1. Найти центр тяжести невесомого стержня длины l , на концах которого укреплены две точечные массы т 1 и т 2 .
| т 1 т 2 l | Решение. Будем искать не центр тяжести, а центр масс (так как это одно и то же). Введем ось х
(рис. 27.3).
|
| х С = ? | |
Ответ : на расстоянии от массы т 1 .
СТОП! Решите самостоятельно: В1–В3.
Утверждение 1. Если однородное плоское тело имеет ось симметрии, центр тяжести находится на этой оси.
Действительно, для всякой точечной массы m i , расположенной справа от оси симметрии, найдется такая же точечная масса , расположенная симметрично относительно первой (рис. 27.4). При этом сумма моментов сил .
Поскольку все тело можно представить разбитым на подобные пары точек, то суммарный момент сил тяжести относительно любой точки, лежащей на оси симметрии равен нулю, а значит, на этой оси находится и центр тяжести тела. Отсюда следует важный вывод: если тело имеет несколько осей симметрии, то центр тяжести лежит на пересечении этих осей (рис. 27.5).
Рис. 27.5 
Утверждение 2 . Если два тела массами т 1 и т 2 соединены в одно, то центр тяжести такого тела будет лежать на отрезке прямой, соединяющей центры тяжести первого и второго тела (рис. 27.6).
Рис. 27.6 ![]() Рис. 27.7
Рис. 27.7
Доказательство. Расположим составное тело так, чтобы отрезок, соединяющий центры тяжести тел был вертикальным. Тогда сумма моментов сил тяжести первого тела относительно точки С 1 равна нулю, и сумма моментов сил тяжести второго тела относительно точки С 2 равна нулю (рис. 27.7).
Заметим, что плечо силы тяжести любой точечной массы т i одно и то же относительно любой точки, лежащей на отрезке С 1 С 2 , а значит, и момент силы тяжести относительно любой точки, лежащей на отрезке С 1 С 2 , один и тот же. Следовательно, сил тяжести всего тела равен нулю относительно любой точки отрезка С 1 С 2 . Таким образом, центр тяжести составного тела лежит на отрезке С 1 С 2 .
Из утверждения 2 следует важный практический вывод, который четко сформулирован в виде инструкции.
Инструкция,
как искать центр тяжести твердого тела, если его можно разбить
на части, положения центров тяжести каждой из которых известно
1. Следует заменить каждую часть массой, расположенной в центре тяжести этой части.
2. Найти центр масс (а это то же самое, что и центр тяжести) полученной системы точечных масс, выбрав удобную систему координат х 0у , по формулам:
В самом деле, расположим составное тело так, чтобы отрезок С 1 С 2 был горизонтальным, и подвесим его на нитях в точках С 1 и С 2 (рис. 27.8,а ). Ясно, что тело будет находиться в равновесии. И это равновесие не нарушится, если мы заменим каждое тело точечными массами т 1 и т 2 (рис. 27.8,б ).
 Рис. 27.8
Рис. 27.8
СТОП! Решите самостоятельно: С3.
Задача 27.2. В двух вершинах равностороннего треугольника помещены шарики массы т каждый. В третьей вершине помещен шарик массы 2т (рис. 27.9,а ). Сторона треугольника а . Определить центр тяжести этой системы.
| т 2т а |  Рис. 27.9
Рис. 27.9
|
| х С = ? у С = ? | |
Решение . Введем систему координат х 0у (рис. 27.9,б ). Тогда
![]() ,
,
 .
.
Ответ : х С = а /2; ; центр тяжести лежит на половине высоты АD .
Последние материалы сайта
Толстой Л.Н.

Проект в детском саду для детей подготовительной группы
Дорогие ребята! Объявляем итоги конкурса детских рисунков «Добрые дела». Победителями стали: I возрастная группа (до 7 лет включительно) 1 место - Александр Виноградов, 7 лет, г. Тихвин «Старость надо уважать. Старшим надо помогать» 2 место - Сева
Горький Максим

Великие князья древней руси и российской империи
Формирование народности, называемой впоследствии русами, русичами, русскими, россиянами, ставшей одной из сильнейших наций в мире, если не самой сильной, началось с объединения славян, расселенных по Восточно-Европейской равнине. Откуда они пришли в эти з
Паустовский К.Г.
Общие закономерности действия на организмы среда и условия существования организмов
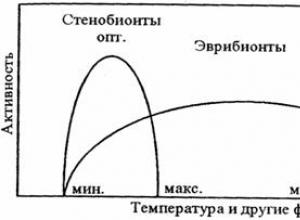
3.1. среда и условия существования организмов Различают такие понятия, как среда и условия существования организмов. Среда - это часть природы, окружающая живые организмы и оказывающая на них прямое или косвенное воздействие. Из среды организмы получают в
Толстой А.Н.

Аудио сказка Снежная королева
Аудиосказка «Снежная Королева» Г.Х. Андерсона можно ставить детям от 3 лет. Это произведение прекрасно убаюкивает малышей, поэтому включать его можно перед сном. В целом сказка имеет отличное музыкальное сопровождение, здесь качественное озвучивание ролей
Сутеев В.Г.

"Несолоно хлебавши": значение фразеологизма, происхождение и толкование Несолоно хлебавши значение фразеологизма
Фразеологизм «несолоно хлебавши», значение которого рассматривается в данной статье, употребляется вместе с глаголом «уйти». Отдельно выражение как-то странно смотрится. Но странность не помешает разобрать его смысл, привести примеры и поведать читателю о
Тургенев И.С.

Басня «Мартышка и очки» (Крылов И
Анализ басни Крылова И.А. «Мартышка и очки» Басня – небольшой рассказ, имеющий чаще всего стихотворную форму, это произведение иронической направленности. Басня – это иносказание, хотя в ней обычно рассказывается о птицах и зверях, но на самом деле в ней